Isaac Newton
From Wikipedia, the free encyclopedia
Godfrey’ Kneller’s 1689 portrait of Isaac Newton
(age 46)
Sir Isaac Newton PRS (25 December 1642 – 20 March 1727 [NS: 4 January 1643 – 31 March 1727]) was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."
His monograph Philosophiæ Naturalis Principia Mathematica, published in 1687, lays the foundations for most of classical mechanics. In this work, Newton described universal gravitation and the three laws of motion, which dominated the scientific view of the physical universe for the next three centuries. Newton showed that the motions of objects on Earth and of celestial bodies are governed by the same set of natural laws, by demonstrating the consistency between Kepler’s laws of planetary motion and his theory of gravitation, thus removing the last doubts about heliocentrism and advancing the Scientific Revolution. The Principia is generally considered to be one of the most important scientific books ever written.
Newton built the first practical reflecting telescope and developed a theory of color based on the observation that a prism decomposes white light into the many colors that form the visible spectrum. He also formulated an empirical law of cooling and studied the speed of sound.
In mathematics, Newton shares the credit with Gottfried Leibniz for the development of differential and integral calculus. He also demonstrated the generalized binomial theorem, developed Newton's method for approximating the roots of a function, and contributed to the study of power series.
Newton was also highly religious. He was an unorthodox Christian, and wrote more on Biblical hermeneutics and occult studies than on science and mathematics, the subjects he is mainly associated with. Newton secretly rejected Trinitarianism, fearing to be accused of refusing holy orders.
Mathematics
Newton's work has been said "to distinctly advance every branch of mathematics then studied".
His work on the subject usually referred to as fluxions or calculus is seen, for example, in a manuscript of October 1666, now published among Newton's mathematical papers. A related subject was infinite series. Newton's manuscript "De analysi per aequationes numero terminorum infinitas" ("On analysis by equations infinite in number of terms") was sent by Isaac Barrow to John Collins in June 1669: in August 1669 Barrow identified its author to Collins as "Mr. Newton, a fellow of our College, and very young ... but of an extraordinary genius and proficiency in these things".
Newton later became involved in a dispute with Leibniz over priority in the development of infinitesimal calculus. Most modern historians believe that Newton and Leibniz developed infinitesimal calculus independently, although with very different notations. Occasionally it has been suggested that Newton published almost nothing about it until 1693, and did not give a full account until 1704, while Leibniz began publishing a full account of his methods in 1684. (Leibniz's notation and "differential Method", nowadays recognized as much more convenient notations, were adopted by continental European mathematicians, and after 1820 or so, also by British mathematicians.) Such a suggestion, however, fails to notice the content of calculus which critics of Newton's time and modern times have pointed out in Book 1 of Newton's Principia itself (published 1687) and in its forerunner manuscripts, such as De motu corporum in gyrum ("On the motion of bodies in orbit"), of 1684. The Principia is not written in the language of calculus either as we know it or as Newton's (later) 'dot' notation would write it. But his work extensively uses an infinitesimal calculus in geometric form, based on limiting values of the ratios of vanishing small quantities: in the Principia itself Newton gave demonstration of this under the name of 'the method of first and last ratios' and explained why he put his expositions in this form, remarking also that 'hereby the same thing is performed as by the method of indivisibles'.
Because of this, the Principia has been called "a book dense with the theory and application of the infinitesimal calculus" in modern times and "lequel est presque tout de ce calcul" ('nearly all of it is of this calculus') in Newton's time. His use of methods involving "one or more orders of the infinitesimally small" is present in his De motu corporum in gyrum of 1684[26] and in his papers on motion "during the two decades preceding 1684".
Newton had been reluctant to publish his calculus because he feared controversy and criticism. He had a very close relationship with Swiss mathematician Nicolas Fatio de Duillier, who from the beginning was impressed by Newton's gravitational theory. In 1691, Duillier planned to prepare a new version of Newton's Principia, but never finished it. However, in 1693 the relationship between the two men changed. At the time, Duillier had also exchanged several letters with Leibniz.
Starting in 1699, other members of the Royal Society (of which Newton was a member) accused Leibniz of plagiarism, and the dispute broke out in full force in 1711. The Royal Society proclaimed in a study that it was Newton who was the true discoverer and labeled Leibniz a fraud. This study was cast into doubt when it was later found that Newton himself wrote the study's concluding remarks on Leibniz. Thus began the bitter controversy, which marred the lives of both Newton and Leibniz until the latter's death in 1716.
Newton is generally credited with the generalized binomial theorem, valid for any exponent. He discovered Newton's identities, Newton's method, classified cubic plane curves (polynomials of degree three in two variables), made substantial contributions to the theory of finite differences, and was the first to use fractional indices and to employ coordinate geometry to derive solutions to Diophantine equations. He approximated partial sums of the harmonic series by logarithms (a precursor to Euler's summation formula), and was the first to use power series with confidence and to revert power series.
He was appointed Lucasian Professor of Mathematics in 1669 on Barrow's recommendation. In that day, any fellow of Cambridge or Oxford was required to become an ordained Anglican priest. However, the terms of the Lucasian professorship required that the holder not be active in the church (presumably so as to have more time for science). Newton argued that this should exempt him from the ordination requirement, and Charles II, whose permission was needed, accepted this argument. Thus a conflict between Newton's religious views and Anglican orthodoxy was averted.
Gottfried Leibniz
From Wikipedia, the free encyclopedia
Gottfried Wilhelm Leibniz (sometimes von Leibniz) (German pronunciation: (Leipzig, July 1, 1646 – Hannover, November 14, 1716) was a German philosopher and mathematician. He wrote in different languages, primarily in Latin (~40%), French (~30%) and German (~15%).
Leibniz occupies a prominent place in the history of mathematics and the history of philosophy. He developed the infinitesimal calculus independently of Isaac Newton, and Leibniz's mathematical notation has been widely used ever since it was published. He became one of the most prolific inventors in the field of mechanical calculators. While working on adding automatic multiplication and division to Pascal's calculator, he was the first to describe a pinwheel calculator in 1685 and invented the Leibniz wheel, used in the arithmometer, the first mass-produced mechanical calculator. He also refined the binary number system, which is at the foundation of virtually all digital computers. In philosophy, Leibniz is mostly noted for his optimism, e.g., his conclusion that our Universe is, in a restricted sense, the best possible one that God could have created. Leibniz, along with René Descartes and Baruch Spinoza, was one of the three great 17th century advocates of rationalism. The work of Leibniz anticipated modern logic and analytic philosophy, but his philosophy also looks back to the scholastic tradition, in which conclusions are produced by applying reason to first principles or prior definitions rather than to empirical evidence. Leibniz made major contributions to physics and technology, and anticipated notions that surfaced much later in biology, medicine, geology, probability theory, psychology, linguistics, and information science. He wrote works on politics, law, ethics, theology, history, philosophy, and philology. Leibniz's contributions to this vast array of subjects were scattered in various learned journals, in tens of thousands of letters, and in unpublished manuscripts. As of 2011, there is no complete gathering of the writings of Leibniz.
Mathematician
Although the mathematical notion of function was implicit in trigonometric and logarithmic tables, which existed in his day, Leibniz was the first, in 1692 and 1694, to employ it explicitly, to denote any of several geometric concepts derived from a curve, such as abscissa, ordinate, tangent, chord, and the perpendicular. In the 18th century, "function" lost these geometrical associations.
Leibniz was the first to see that the coefficients of a system of linear equations could be arranged into an array, now called a matrix, which can be manipulated to find the solution of the system, if any. This method was later called Gaussian elimination. Leibniz's discoveries of Boolean algebra and of symbolic logic, also relevant to mathematics, are discussed in the preceding section. A detailed treatment of Leibniz's writings on the calculus may be found in Bos (1974).
Calculus
Leibniz is credited, along with Sir Isaac Newton, with the inventing of infinitesimal calculus (that comprises differential and integral calculus). According to Leibniz's notebooks, a critical breakthrough occurred on November 11, 1675, when he employed integral calculus for the first time to find the area under the graph of a function y = ƒ(x). He introduced several notations used to this day, for instance the integral sign ∫ representing an elongated S, from the Latin word summa and the d used for differentials, from the Latin word differentia. This cleverly suggestive notation for the calculus is probably his most enduring mathematical legacy. Leibniz did not publish anything about his calculus until 1684. The product rule of differential calculus is still called "Leibniz's law". In addition, the theorem that tells how and when to differentiate under the integral sign is called the Leibniz integral rule.
Leibniz's approach to the calculus fell well short of later standards of rigor (the same can be said of Newton's). We now see a Leibniz proof as being in truth mostly a heuristic argument mainly grounded in geometric intuition. Leibniz also freely invoked mathematical entities he called infinitesimals, manipulating them in ways suggesting that they had paradoxical algebraic properties. George Berkeley, in a tract called The Analyst and elsewhere,[citation needed] ridiculed this and other aspects of the early calculus, pointing out that natural science grounded in the calculus required just as big of a leap of faith as theology grounded in Christian revelation.
From 1711 until his death, Leibniz's life was envenomed by a long dispute with John Keill, Newton, and others, over whether Leibniz had invented the calculus independently of Newton, or whether he had merely invented another notation for ideas that were fundamentally Newton's.
Modern, rigorous calculus emerged in the 19th century, thanks to the efforts of Augustin Louis Cauchy, Bernhard Riemann, Karl Weierstrass, and others, who based their work on the definition of a limit and on a precise understanding of real numbers. While Cauchy still used infinitesimals as a foundational concept for the calculus, following Weierstrass they were gradually eliminated from calculus, though continued to be studied outside of analysis. Infinitesimals survived in science and engineering, and even in rigorous mathematics, via the fundamental computational device known as the differential. Beginning in 1960, Abraham Robinson worked out a rigorous foundation for Leibniz's infinitesimals, using model theory. The resulting non-standard analysis can be seen as a belated vindication of Leibniz's mathematical reasoning.
Now I present you with an instrument I designed to make the understanding of this issue easier. It may also be applied in software.
Note: The pushbar may be turned in order to measure inches.
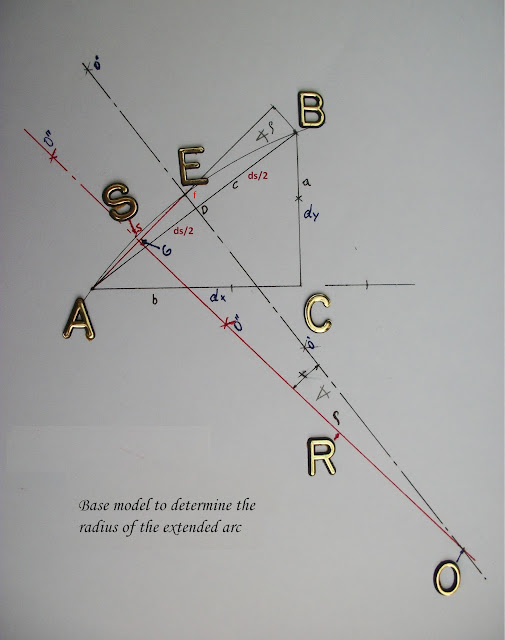
With the instrument, with one spiked leg we puncture vertex A and with the other spiked leg we puncture vertex B of the hypotenuse of extended triangle ABC. Thus, we trace a line of symmetry that is perpendicular to the middle of the hypotenuse AB at D.
Next, with one of the spiked legs of the instrument we puncture vertex A and with the other spiked leg we puncture vertex E of secant - hypotenuse of triangle AED - in order to raise a tangent in the middle of AE at G, intersecting the line of symmetry at 0. 0E is the radius we are looking for.
CONCLUSION
I decided to carry out this research study for I had determined through the equality of perimeters of circumferences and squares that there is no equality of curves and straight lines in the universe that was bequeathed to us. This conclusion was published on page 214 of the book “Resúmenes – de la XVII Reunión Latinoamericana de Matemática Educativa” (Abstracts of the XVII Latin American Meeting on Educational Mathematics) RELME17, Catholic University, Santiago de Chile – July 2003
Abstract
*******************************************PN0505
ANALYSIS OF THE INEQUALITY OF THE CURVE
AND THE STRAIGHT LINE
Structural basis for the extension of the measurement system
Walter Meyer
Research field
Educational level: All levels
“The mathematical relationship of the curve and the straight line is equal, an so it is for squares and circumferences, cubes and spheres.” In simple terms we may say that the same way we operate with squares, we may operate with circumferences and the same way we operate with cubes, we may operate with spheres in an exact manner.
The scheme formed by a circumference and the square formed by its tangents goes from zero to infinite. This is also true for a sphere and the cube formed by its tangential planes. So, we may assert that the definition for the straight line stating that it is an infinite radius curve is false.
The idea is to device a method to measure the whole circular and spherical world EXACTLY, “keeping with the times to come.”
Note: When I name the word “EXACTLY” it refers to geometry and not to measurement systems.
----------------------------------- O -----------------------------------
With numerical working outs on page 7a and 7b, we may see that when we reduce the scale on page 7a to 1,000,000:1, the difference between and arc of circumference and a straight line ds (equal to AB), hypotenuse of triangle ABC, equal to 0.81892113…, the proportion is kept on page 7b (0.000000818921…). We may keep on reducing the scale before reaching 0. (Scale ® 0).
I carried out this study inversely from the study by Mr. Leibniz, so if we could produce computer software, it would consist in:
· Enlarging the characteristic infinitesimal triangles with their corresponding arcs at a scale that would allow us to measure leg dx of the triangle of vertices ABC.
· We then trace secant AE of triangle AED (of legs ds/2 and f = DE)
· At the middle of the secant AE, we raise a perpendicular intersecting the line of symmetry at 0.
· Line segment 0E is the radius of the arc of circumference we are looking for.
NOTE: I have written this study in the simplest way possible in order to get to the largest number of people, most of all college students. I know the subject is sensitive because we know that limits, derivatives, integrals, etc. are concepts.
Published by Walter Meyer
“The idea of the differential notation is an infinitesimal right triangle with legs dx and dy and its hypotenuse being a small curve segment y = f (x) ?. This was the bright idea of Mr. Leibniz.
I will not go into detail on the derivation with the methods of Sir Isaac Newton. You can read about this subject, for we have enough literature and examples in calculus books.
I will neither refer to the problematic of error and linear approximation. I only seek to clarify the concepts so as to obtain computer software that would allow us, through a zoom system, a more real approximation for the calculation we have for a curve.
I believe that the available technology will help us progress more in this issue."





























No hay comentarios:
Publicar un comentario